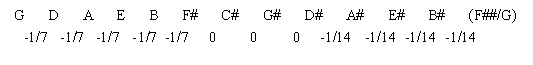We will see that the tuning for Das Wohltemperirte Clavier achieves all of these goals and that, as Lindley intimates, in so doing a finer division of the Pythagorean comma is needed.
Marpurg, while arguing the case for Equal Temperament, noted that there is only one ideal version of this temperament, whereas there are many unequal schemes. He therefore suggested there would be chaos until Equal Temperament was universally achieved, as otherwise each would be inclined to use whatever they considered best. We will see that in Das Wohltemperirte Clavier, J. S. Bach offers a tuning system that is also an ideal of its kind.
J. S. Bach’s use of the generic term ‘Clavier’ (keyboard) leaves unspecified the precise instrument to be used. As noted by Richard Jones, this, in conjunction with the deliberately circumscribed keyboard compass, suggests that the work was intended to be universally accessible to keyboard players regardless of the particular type of instrument (harpsichord, clavichord, or organ) that they might have at their disposal. An important issue arises here, however, in relation to the adoption of an unequal temperament for ‘well-tempered’ instruments; namely coexistence at cammerton and cornet-ton pitch. In the case of equal tempering, this is no concern as each key is identical. However, if unequally tempered instruments at cammerton and cornet-ton pitch are tuned identically to an identical temperament, then there will be inevitable intonation problems as the tuning of one instrument is two places removed from the other on the circle-of-fifths. It follows that there cannot be just one temperament for Das Wohltemperirte Clavier, given the generic term Bach uses, but rather there must be two variants: one for cammerton and another for cornet-ton. We will see that the temperament for Das Wohltemperirte Clavier consists of two transposed cammerton, cornet-ton variants, indicated by respective left-to-right and right-to-left readings of Bach’s diagram.
By virtue of certain telling features in the cammerton and cornet-ton tuning variants, Bach’s scheme can be shown to be an equal-beating one. Its transposition by two places on the circle-of-fifths requires adaptation to one of the beat rates, which Bach explicitly provides. While the equal-beating methods presented by Jorgensen have been viewed cautiously in some circles, they are nevertheless pertinent to Bach’s method. Jorgensen, in his impressive tome, Tuning, traces the historical understanding of beats, noting that in the Seventeenth Century there was no information published that they should increase in frequency when intervals are played higher up the scale. To the musicians at that time, he notes, the quality of the fifths in a scale when played harmonically, seemed identical when their beat frequencies were the same; deceiving them into believing that tempered fifths were of the same size when their beat frequencies were identical. Nor, it seems, had the situation changed by the end of the Eighteenth Century, for in the context of Thomas Young’s rules for well temperament of 1799, Jorgensen notes that it would be authentic practice to apply the much easier equal-beating methods.
C. P. E. Bach writing in 1753 concerning the tuning of the clavichord and harpsichord refers to tempering most of the fifths. He observed that the beats of fifths may be more easily heard by probing fourths. In minimalist terms, he characterised unequal well-tempered tuning:
Both types of instrument must be tempered as follows: In tuning the fifths and fourths, testing minor and major and chords, take away from most of the fifths a barely noticeable amount of their absolute purity. All twenty-four tonalities will thus become usable. The beats of fifths can be more easily heard by probing fourths, an advantage that stems from the fact that the tones of the latter lie closer together than fifths.
Clearly, this generic description does not indicate which fifths should be tempered, nor by how much. Moreover, although one is admonished to listen for the beats of fifths and fourths, there is no indication as to how fast those beats must be in order to take away from the fifth a barely noticeable amount of its absolute purity.
J. S. Bach’s Tuning Procedures
The diagram on the cover sheet of Das Wohltemperirte Clavier, read left-to-right, indicates a tuning scheme for cammerton-pitched instruments. Bearings can be set by proceeding around the circle-of-fifths towards the flats using only fourths and fifths, so as to remain within the octave starting on Middle C. Bach’s diagram indicates three types of interval: i) intervals beating once per second, ii) intervals beating twice per second and iii) pure intervals without beats. In the Eighteenth Century, such tempi could be readily determined from a pocket watch or pendulum clock; today, a metronome at 60 beats per minute will achieve the same result. The protrusion at the left of Bach’s diagram depicts the beat-rate of the interval closing the circle-of-fifths, representing a check that the temperament has been set correctly. That interval arises as a side effect of the tuning scheme, and it beats exactly once per second. A realisation of the tuning procedure constrained to one octave, is illustrated in Figure 1, yielding a temperament denoted as R2-1
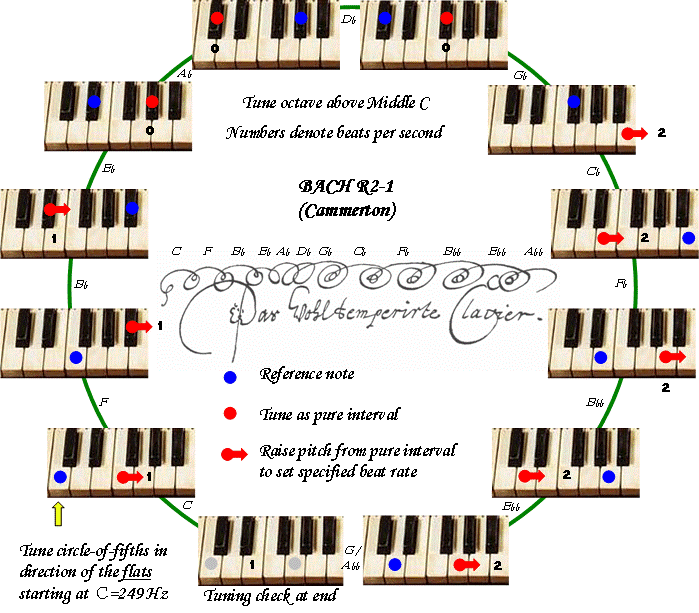
Figure 1: Canonical form of the cammerton tuning procedure
See:
Das Wohltemperirte Clavier - Frequencies
for tuning instruments to the cammerton temperament
An alternative formulation, yielding the same temperament, is presented in Figure 2.

Figure 2: Optimised cammerton tuning procedure using single beat rate of 1 beat per second
Instruments at cornet-ton pitch sound one tone higher than their cammerton counterparts and, to coexist harmoniously in an ensemble, their temperament must be transposed downwards by a whole tone. Read right-to-left, Bach’s diagram yields a transposed tuning scheme for cornet-ton-pitched instruments. Bearings are set by proceeding around the circle-of-fifths towards the sharps, the protrusion at the right of Bach’s diagram giving the expected beat rate for the implicitly tuned interval closing the circle-of-fifths as two beats per second. A realisation of the tuning procedure within one octave is detailed in Figure 3, yielding a temperament denoted as R12-2.
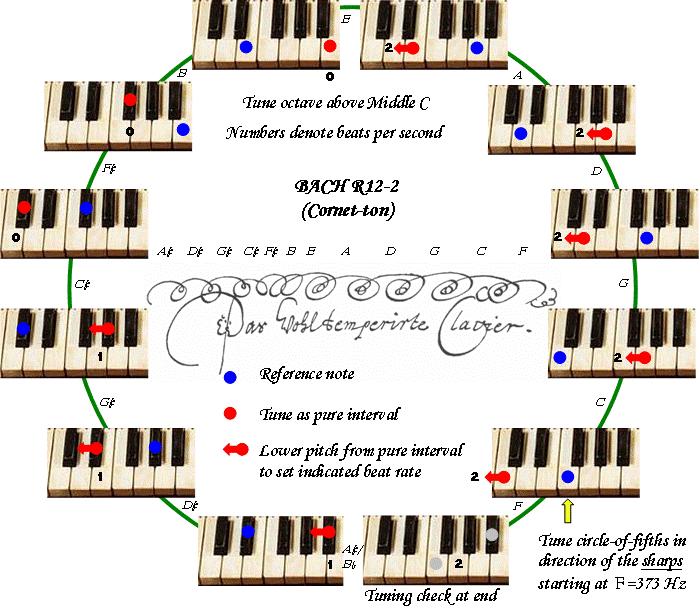
Figure 3: Canonical form of the cornet-ton tuning procedure
Pitch and Temperament
The pitch at which Bach’s tuning procedures were designed can be obtained by reverse-engineering his diagram using the indicated beat rates (see appendices for details). The corresponding temperaments can then be derived from this pitch information. The pitch and temperament are summarised in Table 1 and Table 2, respectively, proving that the circles in Figure 1 and Figure 3 are exact transpositions.
R2-1 (Cammerton) | Frequency (Hz) | R12-2 (Cornet-ton) |
C | 249.072 | |
D@ | 263.154 | |
D | 279.331 | C |
E@ | 296.049 | D@ |
E | 312.998 | D |
F | 332.43 | E@ |
G@ | 350.873 | E |
G | 373.109 | F |
A@ | 394.732 | G@ |
A | 417.997 | G |
B@ | 443.573 | A@ |
B | 468.497 | A |
| 498.145 | B@ |
| 526.309 | B |
Table 1: Pitch of Das Wohltemperirte Clavier
See:
Das Wohltemperirte Clavier - Frequencies
for tuning instruments to the cammerton temperament
R2-1 (Cammerton) | R12-2 (Cornet-ton) |
Note | Temperament (Cents) | Deviation From Equal Temperament (Cents) | Note | Temperament (Cents) | Deviation From Equal Temperament (Cents) |
C | 0 | 0 | | | |
D@ | 95.2136 | - 4.8 | | | |
D | 198.495 | - 1.5 | C | 0 | 0 |
E@ | 299.124 | - 0.9 | D@ | 100.628 | 0.6 |
E | 395.505 | - 4.5 | D | 197.010 | - 3.0 |
F | 499.782 | - 0.2 | E@ | 301.286 | 1.3 |
G@ | 593.259 | - 6.7 | E | 394.763 | - 5.2 |
G | 699.637 | - 0.4 | F | 501.141 | 1.1 |
A@ | 797.169 | - 2.8 | G@ | 598.673 | - 1.3 |
A | 896.314 | - 3.7 | G | 697.818 | - 2.2 |
B@ | 999.128 | - 0.9 | A@ | 800.633 | 0.6 |
B | 1093.770 | - 6.2 | A | 895.273 | - 4.7 |
| | | B@ | 1001.500 | 1.5 |
| | | B | 1096.720 | - 3.3 |
Table 2: Temperament of Das Wohltemperirte Clavier
Temperament Design
The temperament for Das Wohltemperirte Clavier arises naturally as an ideal providing an optimally smooth progression from worst to best thirds across the circle-of-fifths, so satisfying Lindley’s first condition. The thinking that led to its creation can be readily reconstructed from the well known consideration that four consecutive intervals on the circle-of-fifths determine the width of the corresponding major third. The Pythagorean third (~408 cents) is excluded, so that a sequence of four pure fifths does not occur, so satisfying Lindley’s second condition. The widest third must then consist of three consecutive pure intervals on the circle-of-fifths, followed by a tempered interval to narrow the third. This observation yields the sequence 0-0-0-1 on the circle-of-fifths, corresponding to the worst-case third. Optimising for a gradual progression towards better thirds as Lindley suggests, leads to a progressive narrowing of the major thirds by one unit at a time. The results in Table 3 are now predicated.
Tempering of intervals on circle-of-fifths | Narrowing from Pythagorean Third |
(0, 0, 0, 1) | 1 unit |
0, (0, 0, 1, 1) | 2 units |
0, 0, (0, 1, 1, 1) | 3 units |
0, 0, 0, (1, 1, 1, 1) | 4 units |
0, 0, 0, 1, (1, 1, 1, 2) | 5 units |
0, 0, 0, 1, 1, (1, 1, 2, 2) | 6 units |
0, 0, 0, 1, 1, 1, (1, 2, 2, 2) | 7 units |
0, 0, 0, 1, 1, 1, 1, (2, 2, 2, 2) | 8 units |
0, 0, 0, 1, 1, 1, 1, 2, (2, 2, 2, 2) | 8 units |
Table 3: Derivation of Das Wohltemperirte Clavier tuning by progressive narrowing of thirds
Considering the resulting sequence 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 2, it can be seen that the sum of the digits is 14. Accordingly, as the Pythagorean comma must be distributed over the circle-of-fifths, each tempering unit theoretically corresponds to 1/14th part of a Pythagorean comma, the tempering fractions being 1/7 and 1/14. Adopting the historical precedent of placing the best thirds in the key of C, yields the theoretic temperament R12-14P in Figure 4. The equal-beating method for tuning this temperament (R12-2) is depicted in Bach’s diagram, and realised in Figure 3.

Figure 4: R12-14P - theoretic representation of R12-2 in terms of Pythagorean comma fractions
The cornet-ton temperament in Figure 4 must be transposed by a whole tone for cammerton-pitched instruments to give R2-14P as shown in Figure 5.
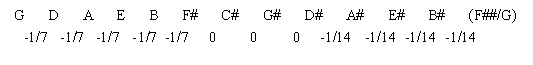
Figure 5: R2-14P - theoretic representation of R2-1 in terms of Pythagorean comma fractions
The equal-beating method for tuning this temperament (R2-1) is depicted in Bach’s diagram, and has been realised in Figure 1 and Figure 2.
The difference in beat rates between cammerton (R2-1) and cornet-ton (R12-2) tuning procedures that occurs at the interval closing the circle-of-fifths, is explicitly represented in Bach’s diagram, and can easily be derived as indicated in Figure 6 from the following well-understood tuning principles:
- An interval without beats in a given octave is without beats in the octave above.
- Inverting a fourth (e.g. C1-F1) such that its lower note sounds an octave higher (i.e. F1-C2 for the given example), yields an interval which beats at the same rate.
- Inverting a fifth (e.g. C1-G1) such that its lower note sounds an octave higher (i.e. G1-C2 for the given example), yields an interval that beats twice as fast.
Cammerton | C | D@ | D | E@ | E | F | G@ | G | A@ | A | B@ | B | C | D@ | Beat Rate |
Loop 1 | C | | | | | F | | | | | | | | | 1 |
Loop 2 | | | | | | F | | | | | B@ | | | | 1 |
Loop 3 | | | | E@ | | | | | | | B@ | | | | 1 |
Loop 4 | | | | E@ | | | | | A@ | | | | | | 0 |
Loop 5 | | D@ | | | | | | | A@ | | | | | | 0 |
Loop 6 | | D@ | | | | | G@ | | | | | | | | 0 |
Loop 7 | | | | | | | G@ | | | | | B | | | 2 |
Loop 8 | | | | | E | | | | | | | B | | | 2 |
Loop 9 | | | | | E | | | | | A | | | | | 2 |
Loop 10 | | | D | | | | | | | A | | | | | 2 |
Loop 11 | | | D | | | | | G | | | | | | | 2 |
Left End | C | | | | | | | G | | | | | | | 1 |
Cornet-ton | | | C | D@ | D | E@ | E | F | G@ | G | A@ | A | B@ | B | |
Loop 1 | | | | | | E@ | | | | | | | B@ | | 1 |
Loop 2 | | | | | | E@ | | | | | A@ | | | | 1 |
Loop 3 | | | | D@ | | | | | | | A@ | | | | 1 |
Loop 4 | | | | D@ | | | | | G@ | | | | | | 0 |
Loop 5 | | | | | | | | | G@ | | | | | B | 0 |
Loop 6 | | | | | | | E | | | | | | | B | 0 |
Loop 7 | | | | | | | E | | | | | A | | | 2 |
Loop 8 | | | | | D | | | | | | | A | | | 2 |
Loop 9 | | | | | D | | | | | G | | | | | 2 |
Loop 10 | | | C | | | | | | | G | | | | | 2 |
Loop 11 | | | C | | | | | F | | | | | | | 2 |
Right End | | | | | | | | F | | | | | B@ | | 2 |
Figure 6: Comparison of the cammerton and cornet-ton tuning procedures.
Intervals in green cross the octave without changing beat rate (fourth is inverted upwards or pure interval).
However, when the interval in red crosses the octave it doubles beat rate since a fifth is inverted upwards.
The respective beat rates of 1 and 2 are captured by the protrusions at the left and right of Bach’s diagram.
Properties of the Derived Tuning Schemes
The properties of the cornet-ton tuning scheme based on 1/14–comma fractions is now compared with the equal beating implementation derived from Bach’s diagram. Figure 7 gives the width of the major thirds, showing a smooth progression from best thirds C-E and F-A to the widest third E-G#. The equal beating scheme tracks the theoretic one closely, generally matching it to within one cent. One exception is E@-G, where the equal beating tuning is almost two cents narrower than theory.
Figure 8 shows the corresponding situation for minor thirds; the best being A-C and D-A, with a progressive narrowing until D@-E. As before, the tracking of the equal beating tuning is generally within one cent, a minor exception being the third G-B@.
Figure 9 shows the width of the fifths; the smallest occurring at C and F, while the largest are at E, B, and F#.
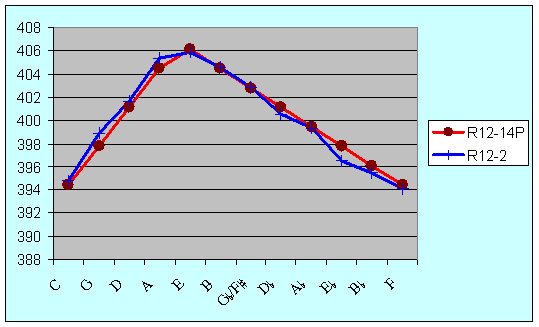
Figure 7: Width of major thirds in cents for R12-14P (theoretic) and R12-2 (equal beating)
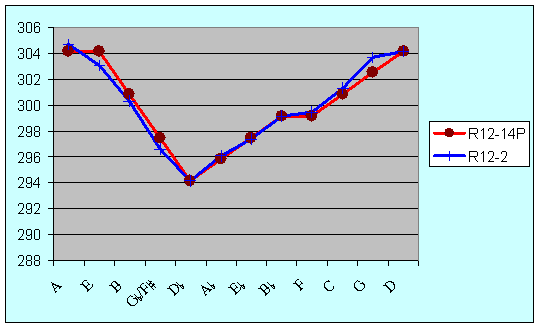
Figure 8: Width of minor thirds in cents for R12-14P (theoretic) and R12-2 (equal beating)
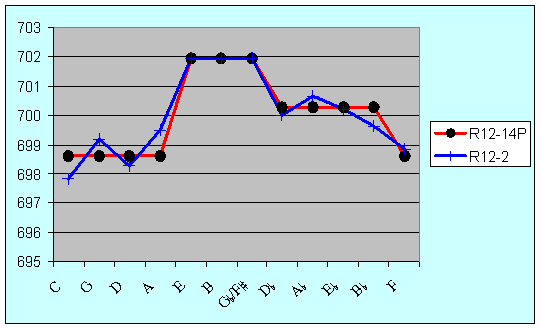
Figure 9: Width of fifths in cents for R12-14P (theoretic) and R12-2 (equal beating)
Comparison with other Temperaments
A comparison of R12-2 (cornet-ton) with other temperaments is given in terms of the Euclidian distance in cents in Figure 10 and in terms of the correlation distance in Figure 11. For the cammerton temperament R2-1, the comparison in terms of Euclidian distance in cents is given in Figure 12, while Figure 13 shows the correlation distance. In terms of correlation distance, the closest match to R12-2 is Zapf, followed by Lehman and Sorge. For R2-1, the closest matches in terms of correlation distance are Neidhardt Circulating No. 1, Sparschuh, Young No. 1, Mercadier and Barnes.
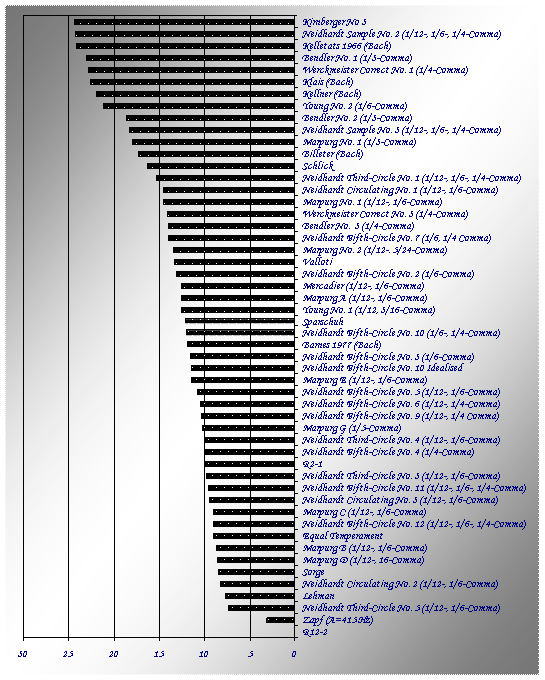
Figure 10: Comparison of R12-2 with other temperaments (Euclidian distance in cents)

Figure 11: Comparison of R12-2 with other temperaments (correlation distance)

Figure 12: Comparison of R2-1 with other temperaments (Euclidian distance in cents)

Figure 13: Comparison of R2-1 with other temperaments (correlation distance)
Approximations to the Tuning Ideal
Noting Lindley’s remarks concerning the inadequacy of a 1/12-comma Pythagorean tempering unit to capture the nuances of Bach’s tuning, it is instructive to consider what happens when Bach’s scheme is represented by other fractions of a comma. For the purpose of comparison and completeness, temperaments are presented for 1/11, 1/12, 1/13, 1/14, 1/15, 1/16, 1/17, 1/18 Pythagorean comma fractions, denoted as R12-11P, R12-12P, R12-13P, R12-14P, R12-15P, R12-16P, R12-17P and R12-18P, respectively. The results are shown in Table 4.
Cents | C | D@ | D | E@ | E | F | G@ | G | A@ | A | B@ | B |
R12-2 | 0.0 | 100.6 | 197.0 | 301.3 | 394.8 | 501.1 | 598.7 | 697.8 | 800.6 | 895.3 | 1001.5 | 1096.7 |
R12-18P | 0.0 | 103.3 | 198.7 | 304.6 | 397.4 | 500.7 | 601.3 | 699.3 | 803.9 | 898.0 | 1005.2 | 1099.3 |
R12-17P | 0.0 | 102.6 | 198.4 | 303.8 | 396.8 | 500.8 | 600.7 | 699.2 | 803.2 | 897.6 | 1004.4 | 1098.7 |
R12-16P | 0.0 | 102.0 | 198.0 | 302.9 | 396.1 | 501.0 | 600.0 | 699.0 | 802.4 | 897.1 | 1003.4 | 1098.0 |
R12-15P | 0.0 | 101.2 | 197.7 | 302.0 | 395.3 | 501.2 | 599.2 | 698.8 | 801.6 | 896.5 | 1002.3 | 1097.3 |
R12-14P | 0.0 | 100.3 | 197.2 | 300.8 | 394.4 | 501.4 | 598.3 | 698.6 | 800.6 | 895.8 | 1001.1 | 1096.4 |
R12-13P | 0.0 | 99.2 | 196.7 | 299.5 | 393.4 | 501.7 | 597.3 | 698.3 | 799.4 | 895.0 | 999.7 | 1095.3 |
R12-12P | 0.0 | 98.0 | 196.1 | 298.0 | 392.2 | 502.0 | 596.1 | 698.0 | 798.0 | 894.1 | 998.0 | 1094.1 |
R12-11P | 0.0 | 96.6 | 195.4 | 296.3 | 390.8 | 502.3 | 594.7 | 697.7 | 796.4 | 893.1 | 996.1 | 1092.7 |
Table 4: Cornet-ton temperaments in cents for different fractions of the Pythagorean comma,
theoretic ideal R12-14P (green) and realisation based on equal-beating tuning R12-2 (yellow)
Table 5 shows the temperaments that occur when other fractions of a comma are used as approximations to Bach’s cammerton tuning. Temperaments are given for 1/11, 1/12, 1/13, 1/14, 1/15, 1/16, 1/17, 1/18 Pythagorean comma fractions, denoted as R2-11P, R2-12P, R2-13P, R2-14P, R2-15P, R2-16P, R2-17P and R2-18P, respectively.
Cents | C | D@ | D | E@ | E | F | G@ | G | A@ | A | B@ | B |
R2-1 | 0.0 | 95.2 | 198.5 | 299.1 | 395.5 | 499.8 | 593.3 | 699.6 | 797.2 | 896.3 | 999.1 | 1093.8 |
R2-18P | 0.0 | 94.1 | 194.8 | 298.0 | 393.5 | 499.3 | 592.2 | 695.4 | 796.1 | 894.1 | 998.7 | 1092.8 |
R2-17P | 0.0 | 94.4 | 195.6 | 298.3 | 394.0 | 499.4 | 592.4 | 696.4 | 796.3 | 894.8 | 998.8 | 1093.2 |
R2-16P | 0.0 | 94.6 | 196.6 | 298.5 | 394.6 | 499.5 | 592.7 | 697.6 | 796.6 | 895.6 | 999.0 | 1093.6 |
R2-15P | 0.0 | 94.9 | 197.7 | 298.8 | 395.3 | 499.6 | 593.0 | 698.8 | 796.9 | 896.5 | 999.2 | 1094.1 |
R2-14P | 0.0 | 95.3 | 198.9 | 299.2 | 396.1 | 499.7 | 593.3 | 700.3 | 797.2 | 897.5 | 999.4 | 1094.7 |
R2-13P | 0.0 | 95.6 | 200.3 | 299.5 | 397.0 | 499.8 | 593.7 | 702.0 | 797.6 | 898.6 | 999.7 | 1095.3 |
R2-12P | 0.0 | 96.1 | 202.0 | 300.0 | 398.0 | 500.0 | 594.1 | 703.9 | 798.0 | 900.0 | 1000.0 | 1096.1 |
R2-11P | 0.0 | 96.6 | 203.9 | 300.5 | 399.3 | 500.2 | 594.7 | 706.2 | 798.6 | 901.6 | 1000.4 | 1097.0 |
Table 5: Cammerton temperaments in cents for different fractions of the Pythagorean comma,
theoretic ideal R2-14P (green) and realisation based on equal-beating tuning R2-1 (yellow)
The major and minor thirds and fifths can now be compared to see the impact of choosing different comma sizes. Only the cornet-ton case need be considered, as cammerton yields identical results under transposition. Moreover, the comparison is restricted to two of the more extreme variants, the 1/12-comma Lehman solution on the one hand and the 1/18-comma interpretation on the other. The progression in the quality of the major thirds from best to worst keys is shown in Figure 14; the minor thirds are given in Figure 15 and the fifths are presented in Figure 16. As can be seen, significant distortion occurs with both 1/12 and 1/18-comma solutions, defeating the ideal of smooth, regular, transitions on the circle-of-fifths. In the case of R12-12P, the major thirds on F, B@, E@, A@, D@ increase in size (reading right to left), but at G@ the third becomes smaller before increasing again at B and finally peaking at E. Comparison with R12-14P shows that this imperfection arises because a 1/14-comma design is being compressed due to a 1/12-comma interpretation. In the minor third case, the behaviour of R12-12P and R12-18P is again arbitrary. In the case of R12-12P, for example, there is a continuous increase in the width of the minor thirds from D@ to B@, but at the next step F there is an out of pattern four cents narrowing, and then the widening continues again until D. Again, comparison with R12-14P shows that this is just a compression artefact due to a reading in terms of a course fractional unit. The 1/12-comma reading in R12-12P results in a wide-fifth, which, as Jorgensen notes, is undesirable harmonic waste (see Tuning). Comparison with R12-14P shows that the imperfection only arises because a 1/14-comma design is being compressed due to a 1/12-comma reading.
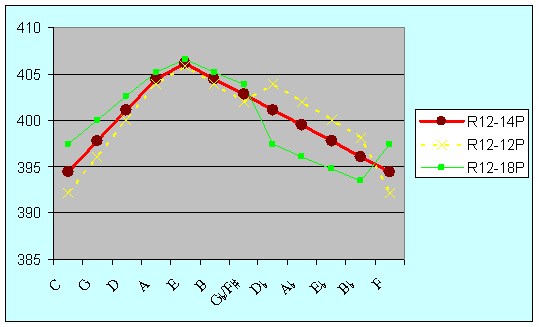
Figure 14: Width of major thirds in R12-14P (theoretic ideal), R12-12P (Lehman) and R12-18P
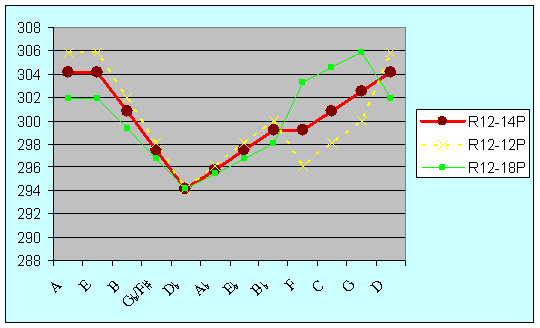
Figure 15: Width of minor thirds in R12-14P (theoretic ideal), R12-12P (Lehman) and R12-18P
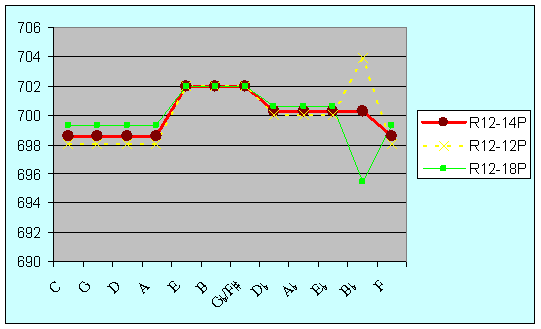
Figure 16: Width of fifths in R12-14P (theoretic ideal), R12-12P (Lehman) and R12-18P
Analysis of Contending Methods
We have seen that a fourteenth part of a Pythagorean comma is the natural basic tempering unit to theoretically describe Bach’s temperament, and that larger fractions compromise the ideal of a progressive gradual change in the size of thirds on the circle-of-fifths, and lead to harmonic waste. The equal-beating methods R2-1 and R12-2, given by respective left-to-right and right-to-left readings of Bach’s diagram, were shown to yield cammerton and cornet-ton transpositions closely approximating the 1/14-comma scheme. The 1/12-comma reading proposed by Lehman was addressed as R12-12P. To complete the picture, the interpretations of Andreas Sparschuh and Michael Zapf will also be considered.
The average minor third must necessarily have a width of 300 cents, the major third 400 cents, and the fifth 700 cents. Improving a third or fifth in one place, must necessarily degrade corresponding intervals elsewhere. The standard deviation, which is a measure of the inequality or colour of a temperament, is shown in Figure 17. R12-14P and R2-14P have the least deviation of the thirds and fifths, while R12-12P (Lehman) has the most. The deviation in the fifths, for example, is some 33% greater, perhaps, making it somewhat harder for singers to hit the right note.
The Zapf and Lehman proposals are essentially variants of the cornet-ton solution R12-14P, while the proposal from Sparschuh is a variant of the cammerton solution R2-14P. The comparison in terms of major thirds is shown in Figure 18. Zapf has a best third F-A comparable to R12-14P and a peak A-C#. R2-14P is simply a displaced version of R12-14P, commencing on cammerton D rather than cornet-ton C. Lehman has a greater tempering of C-E and F-A with a widest third E-G#. His reading further improves the already good thirds of F-A, C-A, G-B and D-A, at the expense of D@-F, A@-C, E@-G and B@-D. The temperament of Sparschuh is broadly comparable to R2-14P, although it wanders around somewhat.
Figure 19 shows the corresponding situation for minor thirds. R12-14P has best minor thirds A-C, E-G, and D-F, with a smooth progression toward the narrowest third D@-E. Zapf has best minor thirds at A-C, with a fairly smooth progression to the narrowest at F#-A. Lehman improves the already good thirds A-C, E-G and D-F at the expense of degrading F-A@, C-E@ and G-B@. His temperament does not exhibit a monotonic rise, as there is an out-of-character drop in width occurring at F-A@. The temperament of Sparschuh is reasonably well-behaved, although not entirely monotonic in ascent.
The sizes of fifths are shown in Figure 20. R12-14 has three sizes of fifth, while Lehman has four including a wide fifth. Both Zapf and Sparschuh use more sizes of fifths.
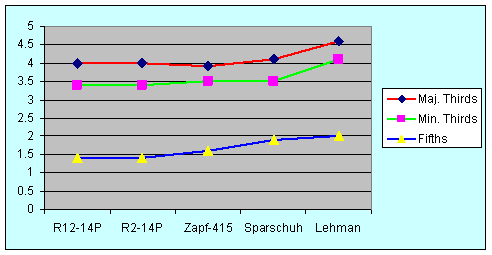
Figure 17: Standard deviation of thirds and fifths (cents)
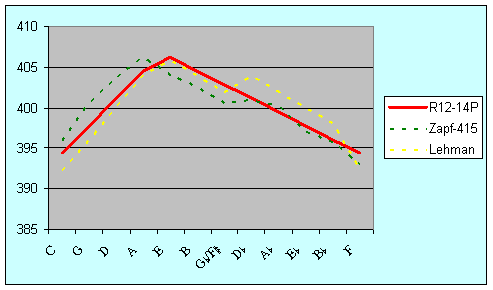
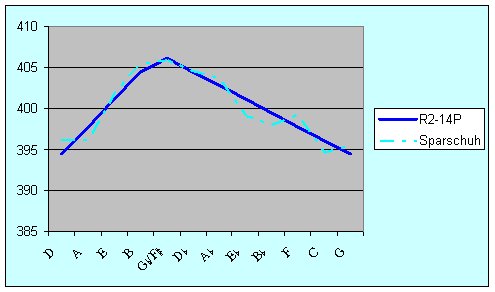
Figure 18: Comparison of major thirds (cents)
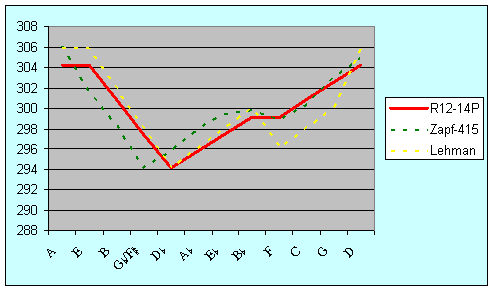
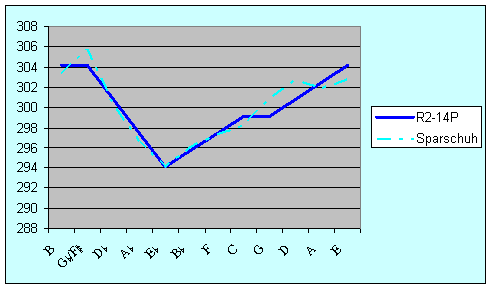
Figure 19: Comparison of minor thirds (cents)
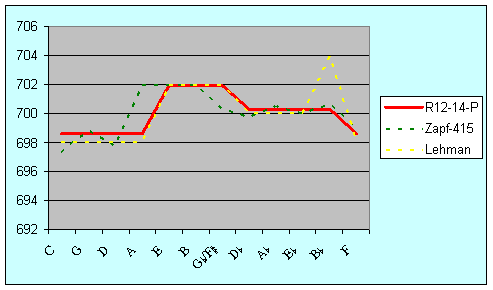
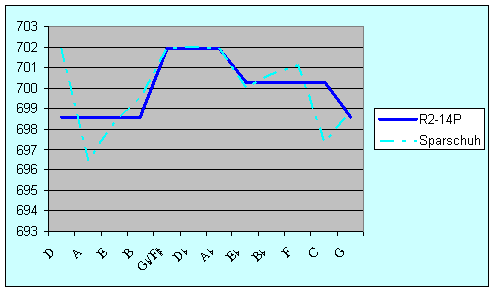
Figure 20: Comparison of fifths (cents)
Conclusions
J. S. Bach’s specification for Das Wohltemperirte Clavier at the top of his 1722 manuscript is a prescriptive tuning method for an equal-beating temperament. The scheme uses an easy-to-set tempo of 1 beat per second. Read left-to-right, the diagram indicates the cammerton tuning procedure for the octave starting on Middle C. The beat rate of the implicitly-tuned interval closing the circle-of-fifths is shown by the left protrusion of Bach’s diagram. Given that stringed instruments need to be regularly tuned, it makes eminent sense that the cammerton tuning should be read from left-to-right and not vice versa. The simple manner by which Bach could determine the relationship between cammerton and cornet-ton beat rates was presented. The cornet-ton tuning also takes place within the octave starting on Middle C, but commences on F, and is based on a right-to-left reading with the implicitly-tuned interval closing the circle-of-fifths at the right. The manner in which cammerton and cornet-ton temperaments have been so combined into one diagram is indeed ingenious.
The rationale behind Bach’s temperament was shown to be an optimally smooth progression in the quality of thirds across the circle-of-fifths. It was shown that the tuning specification in terms of beats is closely linked to a 1/14-comma theoretical scheme, and it was demonstrated that the principles behind the design are violated when a 1/12-comma approximation is used. The 1/14-comma scheme was also compared with the readings of Sparschuh and Zapf. Although all are workable musical solutions, only the 1/14-comma reading achieves the ideal of the temperament design.
The pitches obtained by reverse-engineering Bach’s diagram accord with our current knowledge of historical pitch. The mathematics shows that the octave being tuned is the one based on Middle C, for both cammerton and cornet-ton cases, and that the respective left-to-right and right-to-left readings commence the tuning sequence on C and F, respectively. Optimisations can be made such that intervals that should beat twice per second can be dropped an octave where they beat once per second. Thus, a ‘2’ in Bach’s diagram can be interpreted to mean transpose down one octave and check for a one second beat rate.
An interesting question remains: should one tune in the theoretical manner of R12-14P and R2-14P, or use the equal-beating temperaments R12-2 and R2-1? With choral music, the theoretic form may, perhaps, facilitate better intonation, as fewer intervals are used and all intervals are exact. On the other hand, it may be that certain works of Bach are more authentically rendered by using the equal-beating tuning procedure encoded in Das Wohltemperirte Clavier.
Acknowledgements
The preparation of this article was facilitated by Capella music software and by Yo Tomita’s Bach Musicological Font. Michael Zapf first drew my attention to the important discovery of Andreas Sparschuh, while my interest in Bach’s keyboard temperament was stimulated by the enthusiasm and kindness of the late Herbert Anton Kellner. Special thanks are due to Thomas Braatz for his invaluable assistance and I am also grateful to members of Michael Zapf’s Clavichord Discussion Group for comments received.
Appendix 1: R2-1 Mathematical Analysis
Reduce[{
(* Pitches f0…f11 form an octave, with relationship on
the circle-of-fifths according to Bach's WTC diagram read left
to right *)
3f0 - 2f7 == 1, (* left end: 5th beating once per second *)
3f5 - 4f0 == 1, (* loop 1: 4th beating once per second *)
3f10 - 4f5 == 1, (* loop 2: 4th beating once per second *)
3f3 - 2f10 == 1, (* loop 3: 5th beating once per second *)
3f8 - 4f3 == 0, (* loop 4: pure 4th *)
3f1 - 2f8 == 0, (* loop 5: pure 5th *)
3f6 - 4f1 == 0, (* loop 6: pure 4th *)
3f11 - 4f6 == 2, (* loop 7: 4th beating twice per second *)
3f4 - 2f11 == 2, (* loop 8: 5th beating twice per second *)
3f9 - 4f4 == 2, (* loop 9: 4th beating twice per second *)
3f2 - 2f9 == 2, (* loop 10: 5th beating twice per second *)
3f7 - 4f2 == 2, (* loop 11: 4th beating twice per second *)
(* Cents corresponding to pitch relations *)
c0 == 1200Log[2,1.0],
c1 == 1200Log[2,f1/f0],
c2 == 1200Log[2,f2/f0],
c3 == 1200Log[2,f3/f0],
c4 == 1200Log[2,f4/f0],
c5 == 1200Log[2,f5/f0],
c6 == 1200Log[2,f6/f0],
c7 == 1200Log[2,f7/f0],
c8 == 1200Log[2,f8/f0],
c9 == 1200Log[2,f9/f0],
c10 == 1200Log[2,f10/f0],
c11 == 1200Log[2,f11/f0]},{c1,c2,c3,c4,c5,c6,c7,c8,c9,c10,c11}]
(* Results c0,…,c11 in cents, and f0,…,f11 in Hz *)
c0==0.&&c1==95.2136&&c10==999.128&&c11==1093.77&&c2==198.495&&c3==299.124&&c4==395.505&&c5==499.782&&c6==593.259&&c7==699.637&&c8==797.169&&c9==896.314&&f0==249.072&&f1==263.154&&f10==443.573&&f11==468.497&&f2==279.331&&f3==296.049&&f4==312.998&&f5==332.43&&f6==350.873&&f7==373.109&&f8==394.732&&f9==417.997
Appendix 2: R12-2 Mathematical Analysis
Reduce[{
(* Pitches f0...f11 form an octave with relationship on the
Circle-of-fifths according to Bach's WTC diagram read right to
left *)
3f10 - 4f5 == 2, (* right end: 4th beating twice per second *)
3f5 - 4f0 == 2, (* loop 11: 4th beating twice per second *)
3f0 - 2f7 == 2, (* loop 10: 5th beating twice per second *)
3f7 - 4f2 == 2, (* loop 9: 4th beating twice per second *)
3f2 - 2f9 == 2, (* loop 8: 5th beating twice per second *)
3f9 - 4f4 == 2, (* loop 7: 4th beating twice per second *)
3f4 - 2f11 == 0, (* loop 6: pure 5th *)
3f11 - 4f6 == 0, (* loop 5: pure 4th *)
3f6 - 4f1 == 0, (* loop 4: pure 4th *)
3f1 - 2f8 == 1, (* loop 3: 5th beating once per second *)
3f8 - 4f3 == 1, (* loop 2: 4th beating once per second *)
3f3 - 2f10 == 1, (* loop 1: 5th beating once per second *)
(* Cents corresponding to pitch relations *)
c0 == 1200Log[2,1.0],
c1 == 1200Log[2,f1/f0],
c2 == 1200Log[2,f2/f0],
c3 == 1200Log[2,f3/f0],
c4 == 1200Log[2,f4/f0],
c5 == 1200Log[2,f5/f0],
c6 == 1200Log[2,f6/f0],
c7 == 1200Log[2,f7/f0],
c8 == 1200Log[2,f8/f0],
c9 == 1200Log[2,f9/f0],
c10 == 1200Log[2,f10/f0],
c11 == 1200Log[2,f11/f0]},{c1,c2,c3,c4,c5,c6,c7,c8,c9,c10,c11}]
(* Results c0,…,c11 in cents, and f0,…,f11 in Hz *)
c0==0.&&c1==100.628&&c10==1001.5&&c11==1096.72&&c2==197.01&&c3==301.286&&c4==394.763&&c5==501.141&&c6==598.673&&c7==697.818&&c8==800.633&&c9==895.273&&f0==279.331&&f1==296.049&&f10==498.145&&f11==526.309&&f2==312.998&&f3==332.43&&f4==350.873&&f5==373.109&&f6==394.732&&f7==417.997&&f8==443.573&&f9==468.49